10573. Геометрический
парадокс
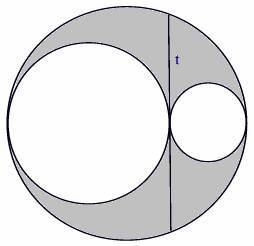
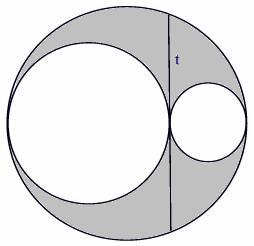
Две малые окружности касаются
друг друга. Большая окружность содержит обе малые как показано на рисунке.
Длина общей хорды равна t. Длины радиусов малых окружностей равны r1 и r2. Центры
всех трех окружностей расположены на одной прямой. Вам заданы значения r1 и r2 или t. Необходимо
найти площадь серой части большей окружности. Если площадь вычислить
невозможно, то вывести “Impossible.”.
Вход. Первая
строка содержит количество тестов n (n ≤ 100). Каждая
следующая строка содержит или два целых числа (r1 и r2) или одно t. Все числа целые, меньше 100.
Выход. Для
каждой входной строки вывести площадь серой части большей окружности..
Пример входа
210 1015 20 Пример выхода
628.3185
1884.9556
РЕШЕНИЕ
геометрия
Анализ алгоритма
Радиус большей окружности равен r = r1 + r2. Если значения r1 и r2 известны, то площадь серой части равна π((r1 + r2)2 – r12 – r22) = 2πr1r2.
Пусть нам известно только
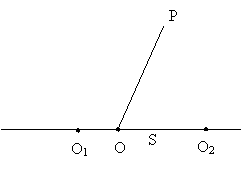
значение t. Рассмотрим прямоугольный
треугольник OPS. В нем OP = r1 + r2, OS = r1 + r2 – 2r2 = r1 – r2, SP = t / 2. Запишем теорему Пифагора:
(r1 + r2)2 = (r1 – r2)2 + t2 /
4
Раскрывая скобки, получим 2 r1 r2 = – 2 r1 r2 + t2 /
4, 4 r1 r2 = t2 /
4.
Площадь серой части равна 2πr1r2 = π t2 / 8.
Реализация алгоритма
Читаем входные данные.
scanf("%d",&n);
while(n--)
{
scanf("%d",&r1);scanf("%c",&c); cnt = 1;
if (c == ' ')
scanf("%d\n",&r2),
cnt = 2;
Вычисляем площадь серой области согласно выше приведенным
формулам.
if (cnt == 2)
res = 2*PI*r1*r2; else res = PI * r1 * r1 / 8;
printf("%.4lf\n",res);
}